Calculation of elastic forces due to large deformations
E = ((ax, bx, cx),
(ay, by, cy),
(az, bz, cz))
α = (E0−1)E
ε = (α+α−I)/2
σ = με + λ(tr ε)I
p = σ(a×b); q = σ(b×c); r = σ(c×a);
Add p dt into momentum at C
Add q dt into momentum at A
Add r dt into momentum at B
Add −(p+q+r) dt into momentum at O
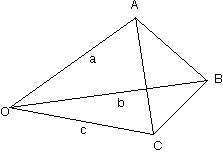
a, b & c are the depicted vector edges of the deformed (strained) zone.
E is a matrix whose components are the components of a, b and c.
E0−1 is precomputed from the unstrained state of
the current zone and is the zone’s shape memory.
α is the affine transformation that takes the unstrained position of the zone into the strained position.
α includes rotation, shear and compression but not translation.
ε is a first order approximation of the strain that is insensitive to rotation.
I is the unit matrix.
tr ε is Σiεii = trace(ε).
λ is the bulk modulus.
μ is the shear modulus.
σ is the stress tensor.
p, q, r are vector forces across zone faces.
The C code is scarcely larger than the above equations as it uses math routines that accept and return scalars, vectors and tensors.
The material moves with the zones—Lagrangian elasto-dynamics.
Norm Hardy
143 Ramona Road
Portola Valley CA, 94028
Ph: 650 851 2582
email: norm at cap-lore dot com

