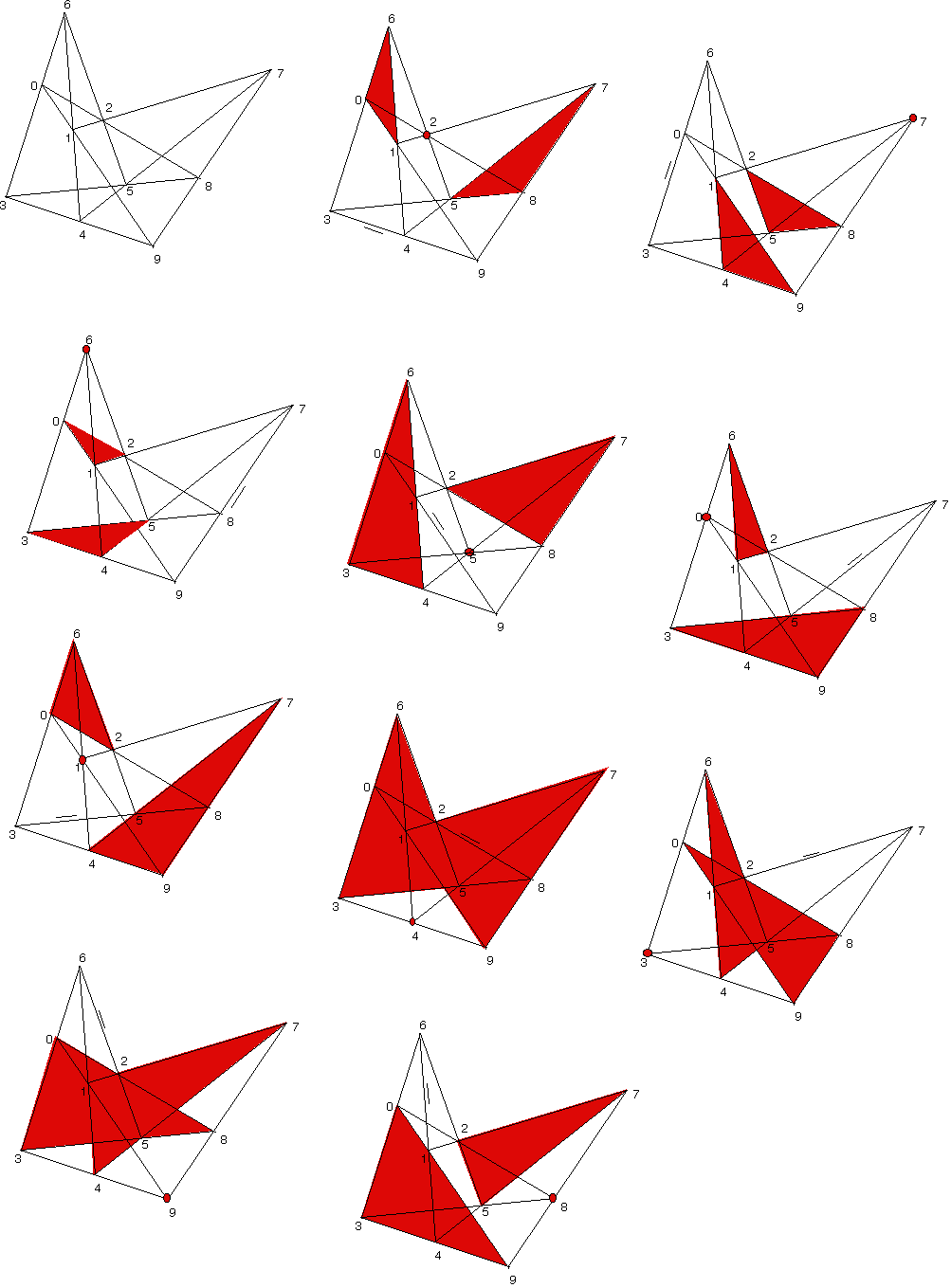
Desargues’ theorem in projective geometry says of two triangles: if lines thru corresponding vertices are concurrent (at point X), then intersections of corresponding sides are collinear. The converse is its dual and thus also a theorem. Below to the left is a diagram illustrating this but without clues about which point is X. Can you tell? All together there are 10 points in the diagram and the symmetry is not immediately obvious. It turns out that 120 of the 10! permutations of these 10 points are equivalent and that any of the 10 points can play the role of X. The other factor of 12 comes from swapping the triangles and permuting the labeling of a triangle. My program tracked down the details. Below are 10 versions of the diagram showing X as a red dot in each, and the corresponding pairs of triangles. There is also a short dash parallel to the line of side intersections. (Nice applets: Tutor, Joyce. An applet revealing the 3D proof)