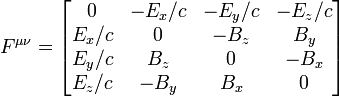Lorentz transformation of Electron’s field

The only relativistic theory I know for the field of a moving point charge is by applying a Lorentz boost A^μ_α to the Electromagnetic tensor:

.
We choose c=1.

A^μ_α =

C S 0 0
S C 0 0
0 0 1 0
0 0 0 1
where C = cosh φ and S = sinh φ .
φ is the ‘rapidity’. The tensor in the boosted frame is F'^μν = A^μ_αA^ν_β F^αβ.

For a motionless point change at the origin sufficient to produce a field of magnitude 1 at distance 1 the field is:
F^αβ = (x² + y² + z²)^–3/2
0 –x –y –z
x 0 0 0
y 0 0 0
z 0 0 0
Consulting this result:
F'^μν = (x² + y² + z²)^–3/2

0 –x –Cy –Cz
x 0 –Sy –Sz
Cy Sy 0 0
Cz Sz 0 0
See this for calculation of F'⁰¹. N.B. the coordinates x, y and z are still those of the point charge’s frame!
t = Ct' – Sx', x = Cx' – St', y = y', z = z'.
and we have:
F'^μν = ((Cx' – St')² + y'² + z'²)^–3/2

0 –(Cx' – St') –Cy' –Cz'
Cx' – St' 0 –Sy' –Sz'
Cy' Sy' 0 0
Cz' Sz' 0 0
The magnetic field is everywhere perpendicular both to the velocity and the displacement vector from the observer to the charge. The point charge is traveling in the x direction. Note that the x component of the magnetic field (F³²) is 0 everywhere. At the event (t', x', y', z') = (0, 0, 0, 1) the electric field is (0, 0, C) and the magnetic field is (0, S, 0). At the event (0, 1, 0, 0) the electric field is (C^–2, 0, 0) and the magnetic field is (0, 0, 0).