Here is how I think about the world, pre quantum and pre Planck.
First there is the real line, R.
R is already pretty spooky—something that you can sub divide indefinitely.
Being able to keep subdividing is probably logically simpler than having to stop somewhere, however.
The Cartesian product R × R × R = R3 which is a lot like space, both as the Greeks idealized it and as used for most engineering.
Two people might agree that the world is R3 without agreeing on the direction that one moves when one of those three numbers change.
(We skip over the easier disagreement as to where to origin is.)
It is not that the world isn’t R3, but that it is R3 in very many different equivalent ways; sort of too much like R3.
There is one thing that R3 doesn’t capture very well—the distance between two points.
Our two theorists can agree on how far apart two things are even when they can’t agree on what direction is North, or even up.
Pythagoras clarified this nicely with his formula:
dist = (dx2 + dy2 + dz2)1/2.
(Pythagoras didn’t have the above notation available, but I am sure that he thought as much.)
Rotations like:| x' = x cos b + y sin b | | y' = − x sin b + y cos b |
| 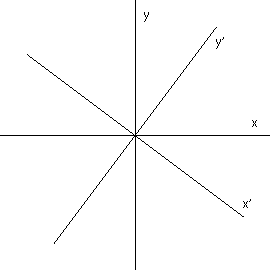 |
didn’t change distances, or the laws of physics.
If the two who couldn’t agree on what is up, both calculated the distance in their respective systems, the result agreed.
This has to do with the fact that rigid bodies can turn in R3 without straining.
Almost no other formula for distance has this property.
No other formula matched the measurements that the Greeks knew how to make.
Euclid’s geometry is all about one place being like another and one direction being like another.
Greek geometry also noted clearly that one size was like another in a certain sense.
I don’t recall that they noted that one time is like another.
Zeno did suggest that time was infinitely divisible in his own way.
With an unsymmetric affine connection objects can change size as well as location.
Galileo made clear that relative motion at speed s, a transformation like
 didn’t change the laws of physics.
He appealed to the experience of those who had been below decks on a moving ship where one cannot sense the motion.
The value of s is inaccessible to the passenger by local experiment.
He thus damaged the intuitive argument that the earth stood still.
Newton started from there preserving Galileo’s idea.
didn’t change the laws of physics.
He appealed to the experience of those who had been below decks on a moving ship where one cannot sense the motion.
The value of s is inaccessible to the passenger by local experiment.
He thus damaged the intuitive argument that the earth stood still.
Newton started from there preserving Galileo’s idea.
Minkowski’s Insight
That whole theory was quite consistent, but alas wrong.
To make a long story short it turns out that space and time are more alike than almost anyone had thought.
There is a transformation that mixes time and space like the transformation above mixes x and y.
Here it is:
| x' = x cosh β + t sinh β | | t' = x sinh β + t cosh β |
|
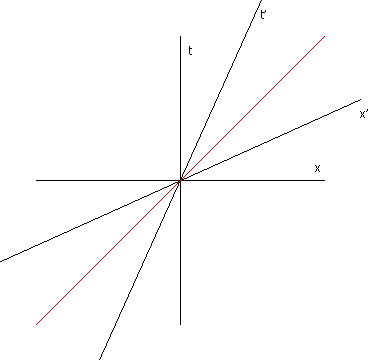 |
Notice the “h” and the end of the trig functions and the missing minus sign.
In the rotation b is the angle.
In the space-time rotation β is called the ‘rapidity’.
When β is small Galileo’s formula is very nearly right and β is very nearly the speed.
The similarity between space and time keeps showing up.
Make no mistake; they are different classes of transformation on R2.
A new quantity: (dt2 − dx2)1/2 is preserved in this
kind of rotation.
It is sort of like distance.
Einstein’s special relativity included stuff also about masses, (E = mc2, etc.), and even electromagnetic fields, but this is all there was to say about space and time.
It is clever that the new relative motion equation is more like spatial rotation, and ultimately it is observationally correct.
Special relativity’s transformation formula is more nearly like Euclid’s formula, than it is like Galileo’s formula.


 didn’t change the laws of physics.
He appealed to the experience of those who had been below decks on a moving ship where one cannot sense the motion.
The value of s is inaccessible to the passenger by local experiment.
He thus damaged the intuitive argument that the earth stood still.
Newton started from there preserving Galileo’s idea.
didn’t change the laws of physics.
He appealed to the experience of those who had been below decks on a moving ship where one cannot sense the motion.
The value of s is inaccessible to the passenger by local experiment.
He thus damaged the intuitive argument that the earth stood still.
Newton started from there preserving Galileo’s idea.
