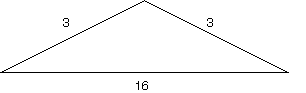
 The above triangle, with indicated (edge length)2s
violates the triangle inequality when roots are taken and produces the metric:
The above triangle, with indicated (edge length)2s
violates the triangle inequality when roots are taken and produces the metric:
We need to understand how signatures of metrics (SMs) of sub simplexes relate to SMs of simplexes. (Maybe not! The following may be on the wrong path. Here is a branch thought.) I think that it is clear that there is a containment relation. Notation: we code (+ + + − −) as SM = (3, 2). I think it is clear that if SM of a simplex is (m, n) and (m', n') is that of a sub-simplex then m' ≤ m and n' ≤ n.
There is another issue.
Our formalism seems oblivious to the triangle inequality and other higher dimensional limitations as to the edge lengths of Euclidean simplexes.
Perhaps some of these (edge length)2 specifications produce Minkowski triangles, even when they are all positive.
Perhaps I will have to compute some eigenvalues.
 The above triangle, with indicated (edge length)2s
violates the triangle inequality when roots are taken and produces the metric:
The above triangle, with indicated (edge length)2s
violates the triangle inequality when roots are taken and produces the metric:
| 1.5 | −5 |
| −5 | 1.5 |
| 1 | 0 |
| 0 | −1 |
| Here is a similar case of a topological tetrahedron in 3D but no Euclidean model: |
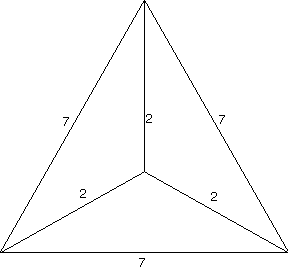 |
I trust that this conjecture protects us from complexes with inhomogeneous signatures.