Hamiltonian Mechanics

Khinchin’s book on statistical mechanics (ISBN=0486601471) introduced me to Hamiltonians. The simple idea there is that H is merely the total energy of the system where H is taken to be some function of the dynamic coordinates p_i and q_i for 1≤i≤s. This idea is evidently in stark contrast to the historical origin of Hamiltonians which is by way of Lagrangians, in terms of which Hamiltonians are normally introduced.

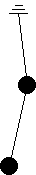
We require:
ṗ_i = ∂H/∂q_i
q̇_i = −∂H/∂p_i
(1)
These two equations provide simple means to compute the evolution of p_i and q_i as time passes. So far we merely have a way to compute the evolution of p’s and q’s if we have a function H of them. H determines the course of the dynamic variables.

Clarification?

I characterize p_i and q_i as positions and momenta respectively for the following but this formalism can be extended to many other physics problems by taking p_i and q_i to be other physical quantities so long as the two equations above hold. (See conjugate coordinates.)

simple oscillator

We consider a simple oscillator first. A mass=m has one degree of freedom x and a spring imposes a force = −hx. Kinetic energy = mx'²/2. When the mass is displaced to x the work against the spring (potential energy) is hx²/2. Using our conventional notions of energy and taking p₁ = x/√h; q₁ = x'/√m
we propose the following Hamiltonian:
H = ((K.E.) + (P.E.)) = ((mx'²/2) + (hx²/2))/2 = (hp₁² + mq₁²)/2.

Note that if H is a serviceable Hamiltonion then so is bH where b is a constant; H and bH predict the same evolution of the dynamic variables but 2H evolves twice as fast as H.

We try ṗ₁ = ∂H/∂q₁ and q̇₁ = −∂H/∂p₁ with our proposed H. ṗ₁ = ∂H/∂q₁ = mq₁ and q̇₁ = −∂H/∂p₁ = −hp₁. These simple differential equations yield:
(p₁, q₁) = (a sin(√(h/m)t + b), a cos(√(h/m)t + b))
for some constants a and b.

Presumably the reader is not yet impressed of the magic of the Hamiltonian; but wait:

compound pendulum

Lets take a compound pendulum (too—better graphics):

Two masses, one beneath the other.
Inelastic links
hinged at the top and at the middle mass
each mass = 1
each link length = 1
g = 1.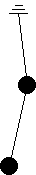

The angle of the upper link relative to the vertical is θ₁ and of the lower link θ₂. p_i = θ_i.

We will need the velocity of the lower weight to compute its kinteic energy. The velocity of the upper weight is d(sin² θ₁,)/dt

H = (K.E.) + (P.E.) = (−2 cos(θ₁) − cos(θ₂)) + (1/2 (θ₁²)