I went to School in Berkeley with Donald Chakerian. I tracked him down in cyberspace and sent him a note about e^δ being a root of 1−3x+3x⁴−x⁵. He immediately noted that τ + √τ is the same root of that polynomial!
τ = (1 + √5)/2 and τ² − τ − 1 = 0. Here is his development:

If τ = (1 + √5)/2 is the Golden Ratio, then τ + √τ = 2.89005363... is a root of x⁵ − 3x⁴ + 3x − 1. In fact

x⁵ − 3x⁴ + 3x − 1 = (x−1)(x⁴ − 2x³ − 2x² − 2x + 1)
= (x−1)(x² + (2τ − 2)x + 1)(x² − 2τx + 1), and
x² − 2τx + 1 = (x − (τ + √τ))(x − (τ − √τ))

Looking in David Kay‘s College Geometry (1969 edition) on page 320, Ex 11, one finds an “equation of Gauss for hyperbolic geometry” that says

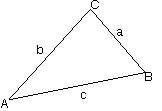
cosh(c/2)sin((A + B)/2) = cosh((a − b)/2)cos(C/2).

in the ∆ABC labeled as on the right

In particular, if ∢A = ∢B = 45° and a = b, this gives

cosh(c/2)/√2 = cos(C/2)

In a right angled regular hyperbolic pentagon, look at the shaded area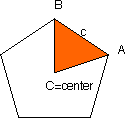
Note that for the shaded ∆ABC we have ∢A = ∢B = 45°, ∢C = 72° and BC = AC. Thus the side c of the pentagon satisfies

cosh(c/2)/√2 = cos 36° = τ/2
or cosh(c/2) = τ/2.

But if

c = ln(τ + √τ)

, I get cosh(c/2) = τ/√2 (use τ² = τ+1).