There is a well known problem and impossibility proof concerning a 2m by 2n array of squares, with two opposite corner squares missing.
Prove that this deficient array cannot be covered by dominoes each of which is the size of two such squares.
The proof requires coloring the array as a checker board.
Assume that the missing squares are red.
Any set of dominoes covers just as many black as red squares, but there are fewer red squares to be covered.
QED.
I think this example is due to John McCarthy, or at least he considered what sorts of artificial intelligence might find the short proofs.
This is a marvelously simple yet in-obvious proof.
It is often stated as an 8 by 8 board but that already suggests a board with a checker pattern.
These proofs are a wonderful examples of a mathematical proof that anyone can understand.
Here is another such problem with another in-obvious proof that is nearly as simple but with a twist.
This time you have a full 2n by 2n array of squares.
You have n2−1 L shape pieces thus:
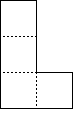
and a 2 by 2 piece thus:
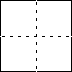
The L’s can be rotated and flipped.
Prove that the 2n by 2n array cannot be covered.
Proof
The trick is again to color the array but differently.
Color the array with parallel stripes alternately black and white—one square wide.
Each L shaped piece covers an odd number of black squares.
The 2 by 2 piece covers an even number of black squares.
There are an odd number of L pieces and thus the collection must cover an odd number of black squares, but there are an even number to be covered.
QED.
This is not my invention.



