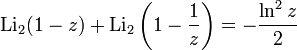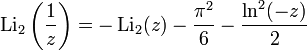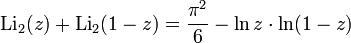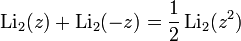A Complex dilogarithm Routine in C
Some dilogarithm references:
Some remarks on this code:
The series is difficult for arguments on the radius of convergence which is the unit circle.
For routine dilogD only 8 digits are expected there or nearby and it can take thousands of terms.
Note the peculiar error in the 8th digit of the test: tst(1, p2/6, "1");.
It would seem that the terms of series beyond 108 sum to just 10−8.
Note that they are all positive and there is thus no cancellation.
This would probably compute twice as many digits.
If we had summed 1016 terms while accumulating terms in ascending magnitudes, we would get a good answer.
Needless to say I have not tried that.
dilog is the current candidate for the dilograthim over the entire complex plane.
The modified series is suggested and derived in the Ginsberg-Zaborowski paper.
The polynomial z2+4z+1 has a root near −0.268 and thus the care to avoid evaluating the series near there.
In both of these cases we exploit the second functional equation in part 2 of Zagier’s useful paper.
The expression (J*J) assumes the successive values of (n(n+1)(n+2))2.
For arguments outside the unit disk we employ the inversion formula which is the first equation of Zagier’s part 2.
In this variation the main routine below tests the code.
Lines 3 and 4 of main verify the surprising functional relations given by Zagier.
The routine tst takes an argument for the dilogarithm, its purported value when known, and an expression for the argument.
It prints the yield of both dilogD and dilog.
Comparison is visual.
Argument 2 is on the cut line in the complex plane and the value there is complex and ambiguous.
Before 2012 Aug 23 Wikipedia said that
Li2(−(1+√5)/2) = −π2/15 + (log(((√5)−1)/2))2/2
which is about −0.5421912164506933 .
Zagier says that the value is
−π2/10 + (log(((√5)+1)/2))2/2 which is the same.
This provides the value −π2/10 − (log(((√5)+1)/2))2 which is about −1.21852526068613 which I presume is correct.
That fits this graph better and I have two independent calculations that corroborate it:
- My program which is a patchwork quilt on the complex plane to avoid awkward regions of convergence and is thus error prone,
but yields −1.2185252606861305,
- but this manifestly simple program to perform the integration yields −1.2185250647848354 .
The integrand is boringly simple and far away from any cut lines and indeed entirely in the conventional real domain of the log function except that log(1−z)/z → −1 as z → 0 from above.
I edited the Wikipedia page and subsequently realized that the only error in the original state of the page was that the values for the following two arguments were exchanged: −(√5+1)/2 and −(√5−1)/2.
I tried to undo my 4 edits that they are not yet undone.
Analytic Continuation, is not too promising.
I think that the 2nd Wikipedia functional equation may support efficient calculation on the radius of convenience when z is near −i.
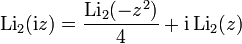 Substituting −iz for z there we get:
Substituting −iz for z there we get:
Li2(z) = Li2(z2)/4 + i Li2(−iz).
Better
Li2(−iz) = i (Li2(z2)/4 − Li2(z)).
Since arguments near 1 and the circle are computed well, we can also compute values on the circle near −i.
Since Li2(z)* = Li2(z*) we can compute Li2 near i too.
The following relation maps the left half of the unit circle onto the highly computable line between ½ ± ½i.
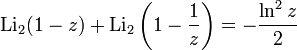
or Li2(z) = − Li2(z / (z − 1)) − (ln(1 − z))2/2
which we corroborate at -0.9+0.12i in one of the ad-hoc tests.
We follow the code:
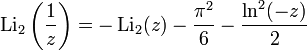
lets us map the entire space outside the unit circle where the series diverges, into it where it converges.
Thus the code beginning if(r > 1) {C r = 1/z;.
It converges inside, even on the circle but quite slowly near the circle.
That is good enough for dilogD but on the circle it takes 108 terms to get 10−16 precision.
Also for the argument 1 there is no cancellation and the truncated part of the series sums to 10−8 — a significant error.
The following formula reflects the whole plane about the line real(z) = ½ and thus we have an easy to avoid a whole region near 1 where the series is troublesome.
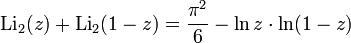
This code does the deed:
if(creal(z) > 0.6) return - dilog(1-z) + p2/6 - (z==1?0:clog(1-z)*clog(z));
The special case of z=1 is because 0 is the limit of the expression as z → 1.
Most of the other trouble areas are in the annulus beyond radius √½.
There are two sub cases there:
Finally when we expelled awkward arguments we use the modified series suggested and derived in the Ginsberg-Zaborowski paper.
The expression (J*J) assumes the successive values of (n(n+1)(n+2))2.
The polynomial z2+4z+1 has a root near −0.268 and thus the care to avoid evaluating the series near there.
Near there the simple series is fine.
This program checks for rough conformance of the numerical derivative of the dilog to theory.
This is a modified version with extensive testing for special cases and performance hooks.
This routine computes only one branch of the dilogrithm.
Others seem obscure.
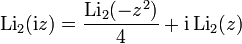 Substituting −iz for z there we get:
Substituting −iz for z there we get: