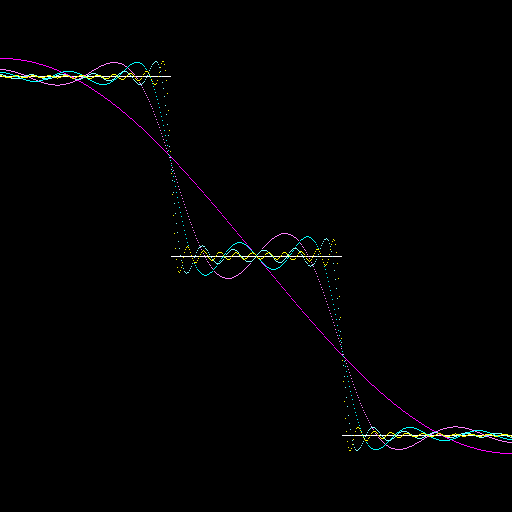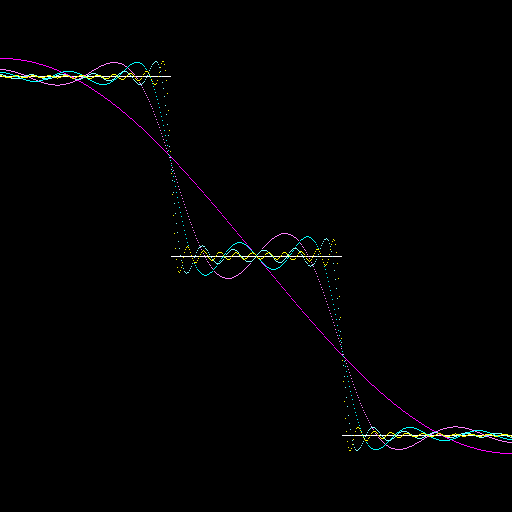
While the triangular initial conditions are fairly realistic, here is a much less realistic square wave initial condition and solution for the same string equation, ∂2y/∂t2 = ∂2y/∂x2.

The string is strung for –π/2≦x≦π/2 the initial boundary conditions for t=0 are: y = 1 for |x| ≦ π/2 and ∂y/∂t = 0. We extend the symmetry as before by declaring that when t=0 and for –∞<x<∞
f(x,0) = –f(x+π,0) and therefore f(x,0) = f(x+2π,0) and f(x,t) = f(–x,t). ∂f(x,t)/∂t = 0. As before f(x,t) = f(x,–t). Now there is a discontinuity when x is an odd multiples of π/2.

The Fourier series for the initial configuration is y = ∑ ancos nx summed over positive integers. Any term in sin nx would violate f(x,t) = f(–x,t).
an = ∫ [–π, π] y cos nx dx/π.
The integral is 0 by symmetry (f(x,0) = –f(x+π,0)) when n is even.

If n is odd then ∫ [–π, π] y cos nx dx/π =
(4/π) ∫ [–π/2, 0] y cos nx dx Each quarter of [–π,π] yields same integral
= (4/π) ∫ [–π/2, 0] cos nx dx Definition of y
= (–1)((n–1)/2)(4/π)/n we skip a few steps

f(x,0) = (4/π)∑ (–1)((n–1)/2) cos(nx)/n summed over odd n. This code corroborates these error prone calculations.

Time Passes

We now consider the time evolution of the string. The shape of the string at time t is f(x,t) = ∑ an(t) cos nx. Each component an(t) cos nx of the Fourier series evolves according to the differential equation and it is easy to see thereby that an(t) = an(0)cos nt. We have thus f(x,t) = ∑ an(0) cos(nx)cos(nt) where
an(0) = an = (–1)((n–1)/2) (4/π)/n of the previous section. Again an(0) = 0 for even n.

This expansion has a slightly different symmetry between t and x. This solution is tested here. Below is the solution ploted for 0<x<π at t=π/6 with approximations 1, 2, 4, 6, 16 and 32. Here is the code.

There is, of course, a quicker way when you have ∂y/∂t = 0 at t = 0.
f(x,t) = (f(x–t,0) + f(x+t,0))/2.