What is a
Homotopy?
Two homeomorphic things are embedded in the same space, but are they embedded the same way?
Two loops on a sphere can be transformed into each other, even if you attend to the question of which way the loop is going.
They are always homotopic, but one loop on a torus will not be deformable into some others.
In general we speak of maps from X to Y.
The image of such a map constitutes an embedding of X in Y if distinct points map to distinct points.
If f0 and f1 both map X into Y then they are said to be homotopic if there is a map F of
[0, 1] × X into Y such that F(0, x) = f0(x) and F(1, x) = f1(x) for all x in X.
The function F(a, x), for some particular a, need not be an embedding, for we do not require that F(a, x1) be different from F(a, x2).
Thus for some a, F(a, x) can map to a single point.
Homotopy is an equivalence relation.
If we choose a point y in Y thru which images of two loops pass and in a neighborhood of y change 
into 
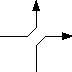then we have a new loop which is perhaps in an equivalence class different from either of the input loops.
This operation defines a group on the homotopic equivalence classes.
If Y is arcwise connected then you can always find representatives of any equivalence class thru any point.
This notion pays attention to the orientation of the loop.
Two rubber bands circling a broomstick in opposite directions cancel each other out when thus multiplied, and the result is homotopic to a point.
They are inverses in the homotopy group.
Wrong!!! The preceding paragraph fell into a trap.
It turns out that it makes a difference homotopically which point you pick to make the splice.
Different choices produce results that are not homotopic to each other!
The easiest counter example is on the punctured torus.
We expand the puncture until it becomes the rectangular border in the pictures below.
In the picture the two dark disks are where the handle recedes behind the plane out of view.
If A is a loop that encircles one end of the handle then it is possible to compute A−1A to be either homotopic to a point or to a loop about the puncture.
These are not homotopic.
If you imagine that the first loop S that girdles a torus the short way and another T goes the long way around, then neither is homotopic with a little loop L.
When you perform this operation on the S and T you get a new loop that is homotopic with none of S, T or L.
Some think that if they know the homotopy group of Y then they know Y.
Here is some evidence.
Here is a very good book on Algebraic Topology.
Wikipedia